2019kaiyun体育（中国）有限公司事业单位考试数量关系解题技巧：统筹问题之空瓶换水

统筹问题在事业单位的考试中是一个常考题型，它是一个利用数学来研究人力、物力的运用和筹划，使他们能发挥最大效率的一类问题。主要包括空瓶换水问题、排队取水问题、真假币问题、过桥问题、货物集中问题等题型。做这种题目的目标是要去找到解决问题的最优方法，结合实际生活考虑就是要做到物尽其用，省时节力。这里主要给大家讲解空瓶换水问题的解题思路。

【例题1】如果5个啤酒空瓶可以换一瓶啤酒，现有24个啤酒空瓶，不交钱最多可以喝( )瓶啤酒。

A.3瓶 B.4瓶 C.5瓶 D.6瓶

【分析】很多同学看到这道题，会简单的就用24除以5等于4余4，也就是能换4瓶啤酒。但大家仔细想一想，如果把换来的4瓶啤酒和剩余的4个空瓶加在一起就会出现8个空瓶，这样还可以再换一瓶啤酒，此时最少也能喝5瓶啤酒，并且还剩余3个空瓶。到这里，很多同学就认为到极限了。其实，为了把资源最大化，换来的第5瓶啤酒喝完也会产生一个空瓶，加上余下的3个空瓶，总共是4个空瓶，如果再来一个空瓶，是不是就可以再喝一瓶啤酒了呢?大家可以试想，先从老板那儿借来一个空瓶，此时就有5个空瓶了，换来一瓶啤酒，喝了之后把瓶再还给老板，这时就可以喝到6瓶啤酒。

当然有同学会想，既然可以借，那就多借点可以喝的更多，但我们要保证借来的瓶子是需要归还的。所以此题对多可以喝到6瓶啤酒。D项正确。

但是，如果每道题目都这样分析的话，就显得很复杂。我们可以把题干中的条件“5个啤酒空瓶可以换一瓶啤酒”可写成恒等式的形式：5个空瓶=1瓶啤酒=1个空瓶+1酒(1酒就只是瓶子里面的酒，不包括瓶子)，两边消去1个空瓶，得：4个空瓶=1酒，那么24除以4就等于6，即最多可以喝6啤酒。

总结：如果m个空瓶可以换1瓶水，现有n个空瓶，最多可以喝到免费的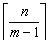瓶水。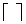代表取整数部分。

【例题2】如果7个矿泉水空瓶可以换2瓶矿泉水，现有25个矿泉水空瓶，不交钱最多可以喝矿泉水( )。

A.8 B.9 C.10 D.11

【答案】C。解析：7空=2空+2水，即5空=2水，25÷5=5次，每次2瓶，共10瓶。 即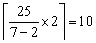，所以D项正确。

【例题3】如果7个矿泉水空瓶可以换3瓶矿泉水，现有25个矿泉水空瓶，不交钱最多可以喝矿泉水( )。

A.18 B.19 C.17 D.20

【答案】A。解析：7空=3空+3水，即4空=3水，25÷4=6次余1瓶，每次3瓶，共18瓶。即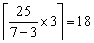

，所以A正确。

总结：如果m个空瓶可以换x瓶水，现有n个空瓶，最多可以喝到免费的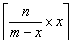瓶水，即：。

只要找到其解题规律，对于同学们来说，空瓶换水问题会快速得出答案。同理，对于统筹问题的任何题型都有相应的解题方法，希望大家都能找到生活中和题目中的最优解。